Publications

2025

1. 

   Nonreciprocal Spin-Glass Transition and Aging

   Giulia Garcia Lorenzana ,  Ada Altieri ,  Giulio Biroli ,  Michel Fruchart ,  and  Vincenzo Vitelli

   Physical Review Letters, 2025

   Abs arXiv paper

   Disordered systems generically exhibit aging and a glass transition. Previous studies have long suggested that non-reciprocity tends to destroy glassiness. Here, we show that this is not always the case using a bipartite spherical Sherrington-Kirpatrick model that describes the antagonistic coupling between two identical complex agents modeled as macroscopic spin glasses. Our dynamical mean field theory calculations reveal an exceptional-point mediated transition from a static disorder phase to an oscillating amorphous phase as well as non-reciprocal aging with slow dynamics and oscillations.

2. 

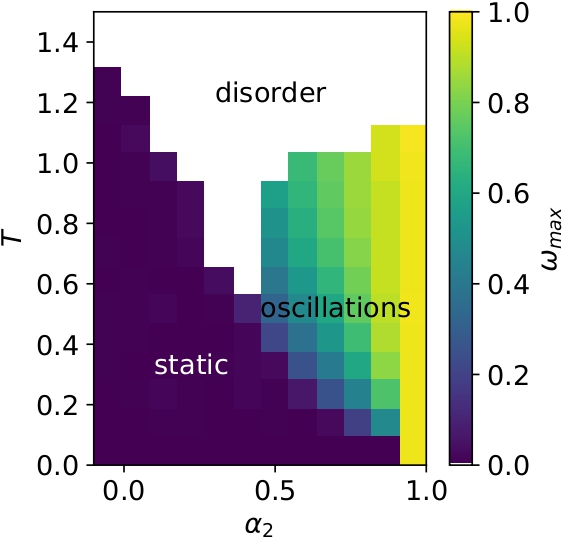   Nonreciprocally coupled spin glasses: Exceptional-point-mediated phase transitions and aging

   Giulia Garcia Lorenzana ,  Ada Altieri ,  Giulio Biroli ,  Michel Fruchart ,  and  Vincenzo Vitelli

   Physical Review E, 2025

   Abs paper

   Disordered systems can exhibit a dramatic slowdown of their dynamics called aging. Contrary to the established understanding that this phenomenon is destroyed by nonreciprocal interactions, we here show that the outcome crucially depends on the structure of the system. Unlike previous studies, which focused on random nonsymmetric interactions between simple microscopic components, we investigate a scenario where nonreciprocally coupled agents are macroscopic entities with complex internal dynamics, modeled as two identical spin glasses. This framework could be relevant for many biological systems, in which nonreciprocal interactions can arise at a coarse-grained level. Our dynamical mean-field theory calculations reveal a finite temperature transition from a static disordered phase to a non-time-translationally-invariant regime. Below this transition, mediated by a spectral singularity known as exceptional points, we find macroscopic oscillations superimposed on aging behavior. Asymptotically, the system rotates in the plane spanned by the two lowest energy modes of the uncoupled system. We contrast these results to the case of random nonreciprocity, where aging is suppressed at any finite temperature, and propose that the two cases correspond to two broader classes of systems, with “microscopic” versus “macroscopic” nonreciprocity, with aging surviving only in the second case.

3. 

   When is nonreciprocity relevant?

   Giulia Garcia Lorenzana ,  David Martin ,  Yael Avni ,  Daniel S. Seara ,  Michel Fruchart ,  Giulio Biroli ,  and  Vincenzo Vitelli

   2025

   Abs arXiv

   Nonreciprocal interactions are widely observed in nonequilibrium systems, from biological or sociological dynamics to open quantum systems. Despite the ubiquity of nonreciprocity, its impact on phase transitions is not fully understood. In this work, we derive criteria to perturbatively assess whether nonreciprocity changes the universality class of pairs of asymmetrically coupled systems undergoing a phase transition. These simple criteria are stated in terms of the unperturbed critical exponents, in the spirit of the Harris criterion for disordered systems, and agree with numerical simulations. Beyond nonreciprocity, our approach provides guidelines for assessing how dynamical phase transitions are affected by perturbations.

2024

1. 

   Corrections to the Bethe lattice solution of Anderson localization

   Matilde Baroni ,  Giulia Garcia Lorenzana ,  Tommaso Rizzo ,  and  Marco Tarzia

   Physical Review B, May 2024

   Abs arXiv paper

   We study numerically Anderson localization on lattices that are tree-like except for the presence of one loop of varying length 𝐿. The resulting expressions allow us to compute corrections to the Bethe lattice solution on (i) random-regular-graph (RRG) of finite-size 𝑁 and (ii) Euclidean lattices in finite dimension. In the first case we show that the prefactor of the 1/𝑁 corrections to the average values of the typical density of states diverges exponentially approaching the critical point. In the second case our results, combined with the 𝑀-layer expansion, predict that corrections destroy the exotic critical behavior of the Bethe lattice solution in any finite dimension, strengthening the suggestion that the upper critical dimension of Anderson localization is infinity. Our approach explains the puzzling observation that the numerical simulations on finite RRGs deviate spectacularly from the expected asymptotic behavior, and opens the way to the computation of non-mean-field critical exponents by resumming the series of diverging diagrams through the same recipes of the field-theoretical perturbative expansion.

2. 

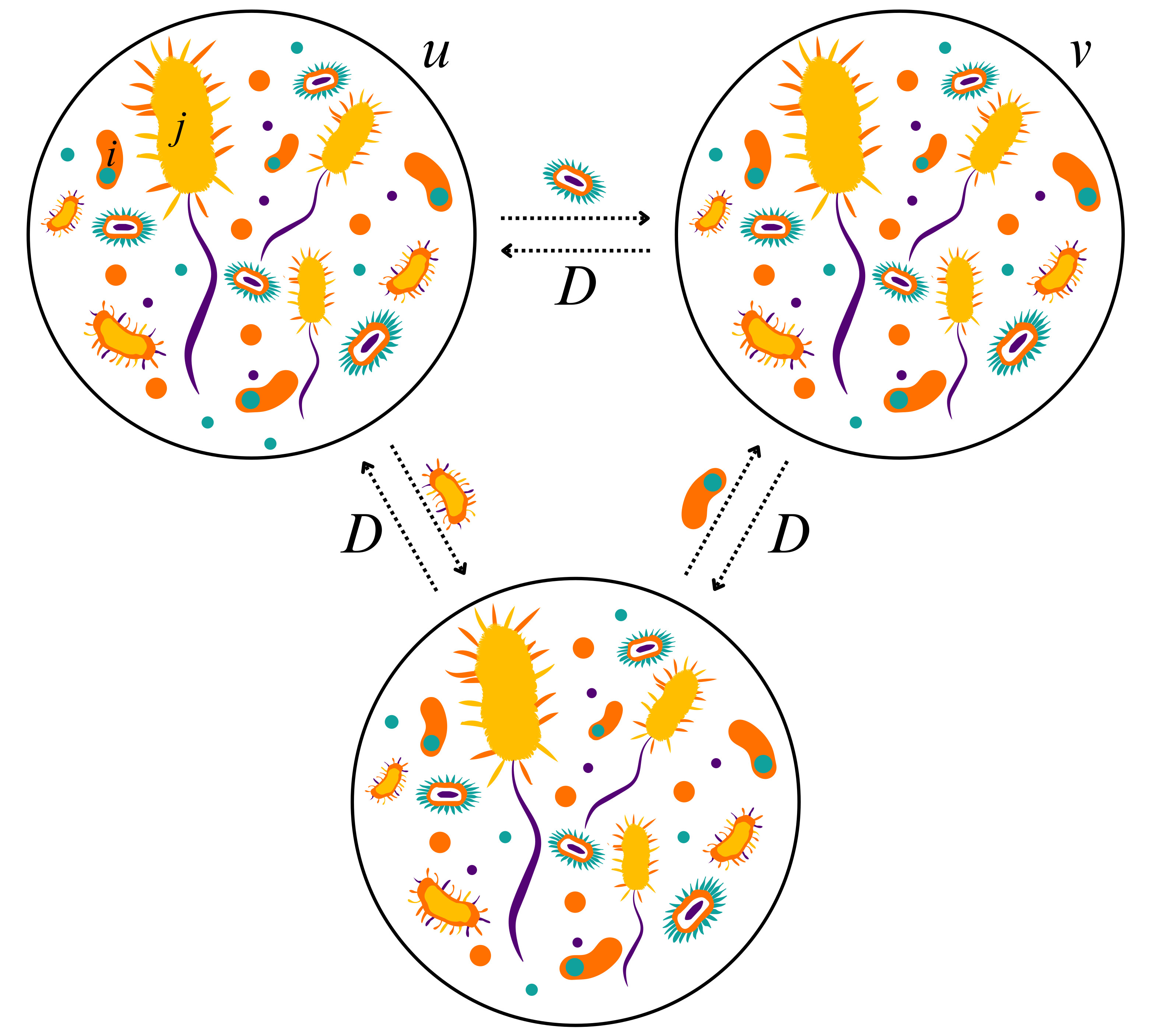   Interactions and Migration Rescuing Ecological Diversity

   Giulia Garcia Lorenzana ,  Ada Altieri ,  and  Giulio Biroli

   PRX Life, Mar 2024

   Abs arXiv open acess paper

   How diversity is maintained in natural ecosystems is a long-standing question in Theoretical Ecology. By studying a system that combines ecological dynamics, heterogeneous interactions, and spatial structure, we uncover a new mechanism for the survival of diversity-rich ecosystems in the presence of demographic fluctuations. For a single species, one finds a continuous phase transition between an extinction and a survival state, that falls into the universality class of Directed Percolation. Here we show that the case of many species with heterogeneous interactions is different and richer. By merging theory and simulations, we demonstrate that with sufficiently strong demographic noise, the system exhibits behavior akin to the single-species case, undergoing a continuous transition. Conversely, at low demographic noise, we observe unique features indicative of the ecosystem’s complexity. The combined effects of the heterogeneity in the interaction network and migration enable the community to thrive, even in situations where demographic noise would lead to the extinction of isolated species. The emergence of mutualism induces the development of global bistability, accompanied by sudden tipping points. We present a way to predict the catastrophic shift from high diversity to extinction by probing responses to perturbations as an early warning signal.

2022

1. 

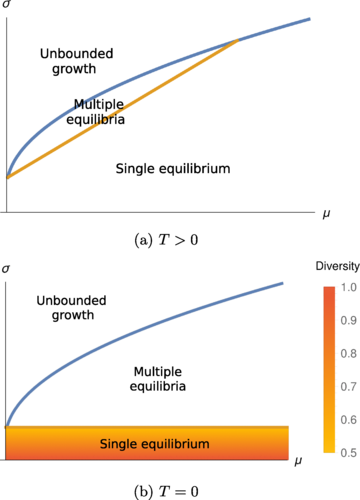   Well-Mixed Lotka-Volterra Model with Random Strongly Competitive Interactions

   G. Garcia Lorenzana ,  and  A. Altieri

   Physical Review E, Feb 2022

   Abs arXiv paper

   The random Lotka-Volterra model is widely used to describe the dynamical and thermodynamic features of ecological communities. In this work, we consider random symmetric interactions between species and analyze the strongly competitive interaction case. We investigate different scalings for the distribution of the interactions with the number of species and try to bridge the gap with previous works. Our results show two different behaviors for the mean abundance at zero and finite temperature, respectively, with a continuous crossover between the two. We confirm and extend previous results obtained for weak interactions: at zero temperature, even in the strong competitive interaction limit, the system is in a multiple-equilibria phase, whereas at finite temperature only a unique stable equilibrium can exist. Finally, we establish the qualitative phase diagrams and compare the species abundance distributions in the two cases.